What Is 3 To The Power Of 3
madrid-atocha
Nov 25, 2025 · 8 min read
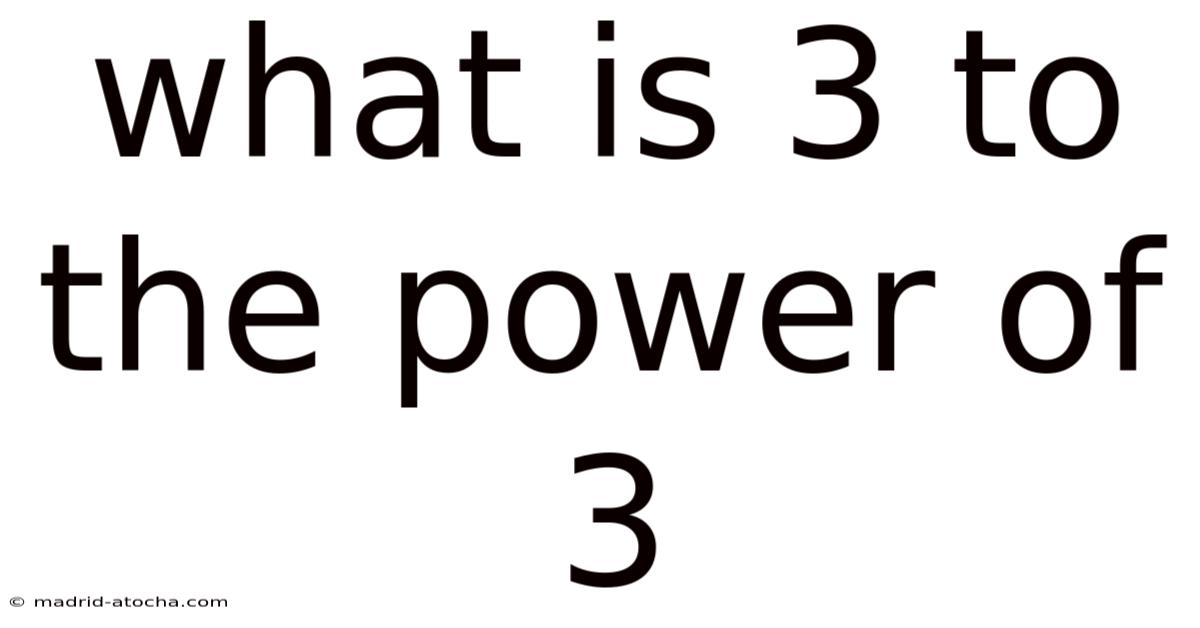
Table of Contents
Let's explore what "3 to the power of 3" means, how to calculate it, and why understanding exponents is so important in mathematics and real-world applications. We'll break down the concept, explore different ways to think about it, and even touch on its broader significance in the world of numbers.
Understanding Exponents
At its core, "3 to the power of 3" is an example of an exponent, also known as a power. Exponents are a shorthand way of expressing repeated multiplication. In the expression a<sup>b</sup> , 'a' is called the base, and 'b' is called the exponent or power. It signifies that 'a' is multiplied by itself 'b' number of times.
So, in the case of "3 to the power of 3" (written as 3<sup>3</sup>), 3 is the base, and 3 is the exponent. This means we multiply 3 by itself three times.
Calculating 3 to the Power of 3
Now that we understand the concept, let's perform the calculation:
3<sup>3</sup> = 3 * 3 * 3
Let's break it down step by step:
- First Multiplication: 3 * 3 = 9
- Second Multiplication: 9 * 3 = 27
Therefore, 3 to the power of 3 equals 27.
Why is this Important?
Understanding exponents is fundamental for several reasons:
- Simplifying Complex Calculations: Exponents allow us to express very large or very small numbers in a compact and manageable form. Imagine trying to write out 2 multiplied by itself 100 times! 2<sup>100</sup> is much easier to handle.
- Scientific Notation: Science relies heavily on exponents through scientific notation. Very large numbers like the speed of light (approximately 300,000,000 meters per second) and very small numbers like the mass of an electron (approximately 0.00000000000000000000000000000091093837 kg) are more easily represented and manipulated using scientific notation, which employs powers of 10.
- Algebra and Beyond: Exponents are a crucial part of algebra, calculus, and many other advanced mathematical fields. They appear in equations, formulas, and models used to describe everything from population growth to radioactive decay.
- Computer Science: Exponents are essential in computer science, especially in dealing with binary numbers (base-2). Understanding powers of 2 is crucial for understanding memory sizes, data storage, and algorithm efficiency.
- Real-World Applications: Exponents are used in various real-world scenarios, including:
- Compound Interest: Calculating the growth of investments over time.
- Population Growth: Modeling how populations increase or decrease.
- Radioactive Decay: Determining the rate at which radioactive substances decay.
- Scaling: Understanding how quantities change when dimensions are scaled (e.g., the relationship between the side length and volume of a cube).
Exploring Different Perspectives
Let's look at "3 to the power of 3" from a few different angles to solidify our understanding:
- Geometric Interpretation: Think of a cube. If each side of the cube has a length of 3 units, then the volume of the cube is 3 * 3 * 3 = 27 cubic units.
- Combinatorial Interpretation: Imagine you have three choices to make, and for each choice, you have three options. The total number of possible outcomes is 3 * 3 * 3 = 27. For example, if you're choosing an outfit and have 3 shirts, 3 pants, and 3 hats, you have 27 different outfit combinations.
- Pattern Recognition: Consider the powers of 3:
- 3<sup>0</sup> = 1
- 3<sup>1</sup> = 3
- 3<sup>2</sup> = 9
- 3<sup>3</sup> = 27
- 3<sup>4</sup> = 81 Notice how each power of 3 is obtained by multiplying the previous power by 3.
Expanding Our Knowledge of Exponents
Now that we've mastered "3 to the power of 3," let's broaden our understanding of exponents in general.
Basic Rules of Exponents:
- Product of Powers: a<sup>m</sup> * a<sup>n</sup> = a<sup>m+n</sup>. When multiplying powers with the same base, you add the exponents. For example, 2<sup>2</sup> * 2<sup>3</sup> = 2<sup>5</sup> = 32.
- Quotient of Powers: a<sup>m</sup> / a<sup>n</sup> = a<sup>m-n</sup>. When dividing powers with the same base, you subtract the exponents. For example, 5<sup>4</sup> / 5<sup>2</sup> = 5<sup>2</sup> = 25.
- Power of a Power: (a<sup>m</sup>)<sup>n</sup> = a<sup>mn</sup>*. When raising a power to another power, you multiply the exponents. For example, (4<sup>2</sup>)<sup>3</sup> = 4<sup>6</sup> = 4096.
- Power of a Product: (ab)<sup>n</sup> = a<sup>n</sup>b<sup>n</sup>. The power of a product is the product of the powers. For example, (2*3)<sup>2</sup> = 2<sup>2</sup> * 3<sup>2</sup> = 4 * 9 = 36.
- Power of a Quotient: (a/b)<sup>n</sup> = a<sup>n</sup>/b<sup>n</sup>. The power of a quotient is the quotient of the powers. For example, (6/2)<sup>2</sup> = 6<sup>2</sup> / 2<sup>2</sup> = 36 / 4 = 9.
- Zero Exponent: a<sup>0</sup> = 1 (where a ≠ 0). Any non-zero number raised to the power of 0 equals 1. For example, 7<sup>0</sup> = 1.
- Negative Exponents: a<sup>-n</sup> = 1/a<sup>n</sup>. A negative exponent indicates the reciprocal of the base raised to the positive exponent. For example, 2<sup>-3</sup> = 1/2<sup>3</sup> = 1/8.
- Fractional Exponents: a<sup>m/n</sup> = <sup>n</sup>√a<sup>m</sup>. A fractional exponent represents a root. For example, 4<sup>1/2</sup> = √4 = 2 (square root of 4), and 8<sup>1/3</sup> = <sup>3</sup>√8 = 2 (cube root of 8).
Advanced Concepts:
- Exponential Functions: An exponential function is a function of the form f(x) = a<sup>x</sup>, where 'a' is a constant base. These functions are used to model exponential growth and decay, which occur in many natural and social phenomena.
- Logarithms: Logarithms are the inverse of exponential functions. The logarithm of a number 'x' to the base 'a' (written as log<sub>a</sub>x) is the exponent to which 'a' must be raised to produce 'x'. Logarithms are used to solve equations involving exponents and in various applications, such as measuring the intensity of earthquakes (the Richter scale) and the loudness of sounds (decibels).
- Complex Exponents: Exponents can also be applied to complex numbers, leading to fascinating results described by Euler's formula: e<sup>ix</sup> = cos(x) + isin(x)*, where 'e' is Euler's number (approximately 2.71828), 'i' is the imaginary unit (√-1), and 'x' is a real number.
Practical Examples and Exercises
To further solidify your understanding, let's look at some practical examples and exercises:
Example 1: Compound Interest
Suppose you invest $1000 in an account that earns 5% interest compounded annually. How much will you have after 3 years?
The formula for compound interest is: A = P(1 + r/n)<sup>nt</sup>
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount) = $1000
- r = the annual interest rate (as a decimal) = 0.05
- n = the number of times that interest is compounded per year = 1
- t = the number of years the money is invested or borrowed for = 3
So, A = 1000(1 + 0.05/1)<sup>1*3</sup> = 1000(1.05)<sup>3</sup> = 1000 * 1.157625 = $1157.63 (approximately)
Example 2: Population Growth
A population of bacteria doubles every hour. If you start with 100 bacteria, how many will there be after 5 hours?
The formula for exponential growth is: N(t) = N<sub>0</sub> * 2<sup>t</sup>
Where:
- N(t) = the population at time 't'
- N<sub>0</sub> = the initial population = 100
- t = the time in hours = 5
So, N(5) = 100 * 2<sup>5</sup> = 100 * 32 = 3200 bacteria
Exercises:
- Calculate 4<sup>3</sup>.
- Simplify: (2<sup>3</sup> * 2<sup>4</sup>) / 2<sup>2</sup>.
- Evaluate: 9<sup>1/2</sup>.
- Solve for x: 3<sup>x</sup> = 81.
- What is the value of 5<sup>0</sup>?
Common Mistakes to Avoid
While exponents are relatively straightforward, here are some common mistakes to watch out for:
- Confusing Exponents with Multiplication: Remember that a<sup>b</sup> means multiplying 'a' by itself 'b' times, not multiplying 'a' by 'b'. For example, 3<sup>3</sup> is 3 * 3 * 3 = 27, not 3 * 3 = 9.
- Incorrectly Applying the Order of Operations: Remember the order of operations (PEMDAS/BODMAS): Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right). Exponents should be evaluated before multiplication, division, addition, and subtraction.
- Forgetting the Rules for Negative Exponents: A negative exponent indicates a reciprocal. a<sup>-n</sup> = 1/a<sup>n</sup>.
- Misunderstanding Fractional Exponents: A fractional exponent represents a root. a<sup>1/n</sup> is the nth root of 'a'.
- Assuming a<sup>m</sup> + a<sup>n</sup> = a<sup>m+n</sup>: This is incorrect. The rule a<sup>m</sup> * a<sup>n</sup> = a<sup>m+n</sup> applies to multiplication, not addition. There's no simple rule for simplifying a<sup>m</sup> + a<sup>n</sup>.
Conclusion
Understanding exponents, like "3 to the power of 3," is a cornerstone of mathematical literacy. It's not just about memorizing rules; it's about grasping the underlying concept of repeated multiplication and its far-reaching implications. From simple calculations to complex scientific models, exponents are an indispensable tool for understanding and describing the world around us. By mastering the basics and exploring advanced concepts, you'll unlock a deeper appreciation for the power and elegance of mathematics. So, keep practicing, keep exploring, and keep expanding your knowledge of exponents!
Latest Posts
Latest Posts
-
What Is Nice To Meet You In Spanish
Dec 03, 2025
-
How Do U Say Me To In Spanish
Dec 03, 2025
-
How Was Your Day In Japanese
Dec 03, 2025
-
Have A Good Day In Polish
Dec 03, 2025
-
What Is The Difference Between Receipt And Invoice
Dec 03, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 To The Power Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.