What Is 2/3 Of 2/3 Cup
madrid-atocha
Dec 06, 2025 · 9 min read
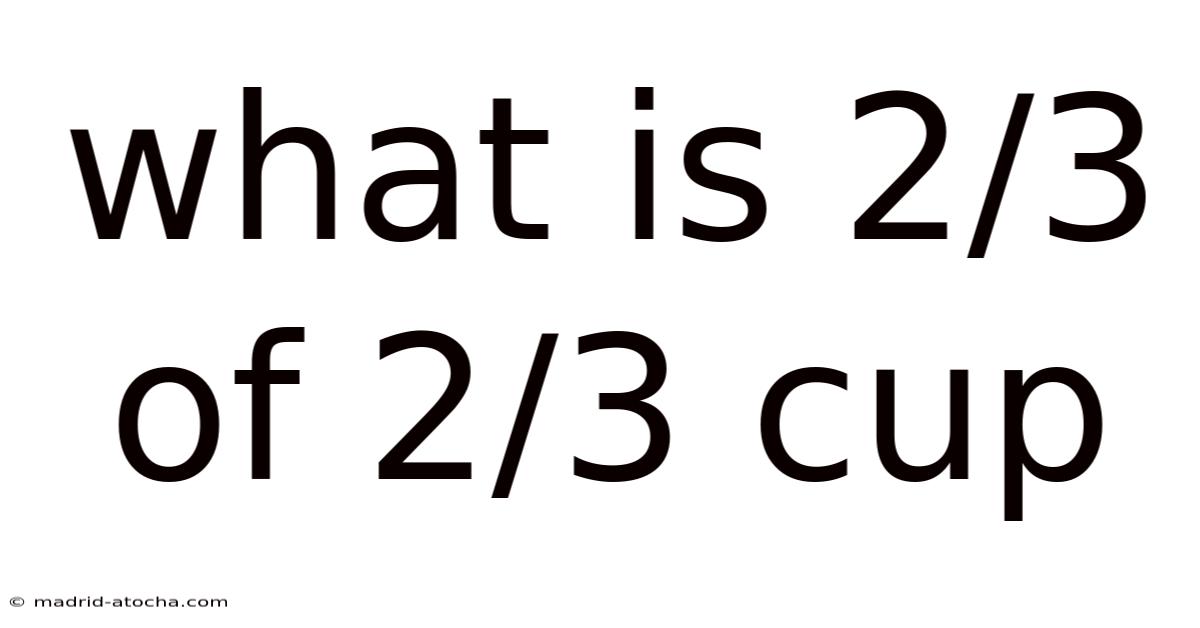
Table of Contents
Calculating 2/3 of 2/3 Cup: A Comprehensive Guide
The question "What is 2/3 of 2/3 cup?" is a common mathematical problem that arises in various real-life situations, particularly in cooking and baking. This article provides a detailed explanation of how to calculate fractions of fractions, offering step-by-step instructions, practical examples, and a scientific perspective to ensure a thorough understanding. Whether you're a student learning fractions or a home cook adjusting a recipe, this guide will equip you with the knowledge and skills to solve such problems with confidence.
Introduction
Understanding fractions is fundamental to mathematics and essential for everyday tasks. Calculating a fraction of a fraction involves multiplying two fractions together. In this case, we want to find 2/3 of 2/3 cup. This type of problem is often encountered when scaling recipes, measuring ingredients, or dealing with proportions. By the end of this guide, you’ll know exactly how to perform this calculation and apply it to various scenarios.
Breaking Down the Problem
What Does "Of" Mean in Mathematics?
In mathematical terms, the word "of" often indicates multiplication. Therefore, "2/3 of 2/3" means we need to multiply 2/3 by 2/3.
Understanding Fractions
A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates the total number of parts the whole is divided into.
For example, in the fraction 2/3:
- The numerator (2) tells us we have 2 parts.
- The denominator (3) tells us the whole is divided into 3 parts.
Step-by-Step Calculation
To find 2/3 of 2/3 cup, follow these simple steps:
Step 1: Write Down the Problem
First, write down the problem as a mathematical expression:
2/3 of 2/3 = 2/3 × 2/3
Step 2: Multiply the Numerators
Multiply the numerators (the top numbers) of the two fractions:
2 × 2 = 4
Step 3: Multiply the Denominators
Multiply the denominators (the bottom numbers) of the two fractions:
3 × 3 = 9
Step 4: Write the Resulting Fraction
Combine the new numerator and the new denominator to form the resulting fraction:
4/9
Step 5: Include the Unit
Since we're calculating a fraction of a cup, we need to include the unit in our answer:
2/3 of 2/3 cup = 4/9 cup
Therefore, 2/3 of 2/3 cup is equal to 4/9 cup.
Practical Examples and Applications
Scaling Recipes
Imagine you are baking a cake, and the original recipe calls for 2/3 cup of flour. However, you only want to make 2/3 of the recipe. To find out how much flour you need, you calculate 2/3 of 2/3 cup:
Flour needed = 2/3 × 2/3 cup = 4/9 cup
So, you will need 4/9 cup of flour for your scaled-down recipe.
Measuring Ingredients
Suppose you have a measuring cup that is divided into thirds, and you need to measure 2/3 of 2/3 cup of sugar. You can use the calculation we just performed to determine that you need 4/9 cup of sugar. This means you need to fill the measuring cup to a point that represents 4/9 of the total volume.
Real-World Scenario: Mixing Paint
Let's say an artist needs to mix a specific color by using 2/3 of 2/3 cup of blue paint. By calculating 2/3 of 2/3 cup, the artist knows exactly how much blue paint to use, ensuring the color mixture is accurate and consistent.
Converting Fractions to Other Units
Converting to Tablespoons
Sometimes, it might be easier to measure 4/9 cup in tablespoons. To convert cups to tablespoons, we use the conversion factor:
1 cup = 16 tablespoons
Therefore:
4/9 cup = 4/9 × 16 tablespoons = 64/9 tablespoons ≈ 7.11 tablespoons
So, 4/9 cup is approximately equal to 7.11 tablespoons. Since it's hard to measure 0.11 of a tablespoon, you can round it to the nearest measurable amount, like 7 tablespoons plus a little extra.
Converting to Milliliters
If you prefer using milliliters, you can convert cups to milliliters using the conversion factor:
1 cup ≈ 236.59 milliliters
Therefore:
4/9 cup = 4/9 × 236.59 ml ≈ 105.15 ml
Thus, 4/9 cup is approximately equal to 105.15 milliliters. This conversion can be useful in precise scientific or culinary applications.
Visual Representation
Using Diagrams
A visual representation can make understanding fractions easier. Consider a square divided into 3x3 grid, making 9 equal parts. Each part represents 1/9 of the whole. If you shade 4 of these parts, you visually represent 4/9. This visual aid helps in understanding that 4/9 is less than half of the whole (which would be 4.5/9).
Using Pie Charts
Another visual aid is a pie chart. Imagine a pie cut into 9 equal slices. If you take 4 of those slices, you have 4/9 of the pie. This visual representation can be particularly helpful for those who learn better through visual aids.
Tips and Tricks for Fraction Calculations
Simplifying Fractions
Before multiplying, check if the fractions can be simplified. Simplifying fractions makes the multiplication easier. In our example, 2/3 and 2/3 are already in their simplest form, so no simplification is needed.
Cross-Cancellation
In some cases, you can use cross-cancellation to simplify multiplication. However, in our case, cross-cancellation is not applicable because there are no common factors between the numerators and denominators of the fractions.
Estimation
Estimating the result can help you check if your answer is reasonable. Since 2/3 is a bit more than half, 2/3 of 2/3 should be a bit more than half of 2/3. Half of 2/3 is 1/3, so our answer of 4/9 is a reasonable estimation.
Common Mistakes to Avoid
Misunderstanding "Of"
A common mistake is not recognizing that "of" means multiplication. Always remember that when you see "of" between two fractions or a fraction and a whole number, it indicates multiplication.
Incorrect Multiplication
Ensure you multiply the numerators together and the denominators together separately. Mixing these up can lead to incorrect results.
Forgetting the Unit
Always include the unit (e.g., cup, tablespoon, milliliter) in your final answer to provide context and meaning to the numerical result.
Not Simplifying
Failing to simplify fractions before or after multiplication can lead to larger, more complex fractions that are harder to work with. Always simplify when possible.
The Scientific Explanation
The Mathematical Principle
Multiplying fractions is based on the principle of dividing a portion into further portions. When we calculate 2/3 of 2/3, we are essentially taking 2 parts out of 3 and then taking 2 parts out of those 3 parts.
Fraction Multiplication as Area
Another way to understand fraction multiplication is through the concept of area. Imagine a square with sides of length 1. If you divide one side into three equal parts and shade two of those parts, you have 2/3 of the square’s length. Now, divide the adjacent side into three equal parts and shade two of those parts as well. The overlapping area represents 2/3 of 2/3 of the square, which is 4/9 of the total area.
Fraction Multiplication in Set Theory
In set theory, multiplying fractions can be seen as finding the intersection of two fractional parts of a whole. If you have a set representing 2/3 of a whole and you want to find 2/3 of that set, you are essentially finding the intersection, which results in 4/9 of the original whole.
Advanced Concepts
Multiplying More Than Two Fractions
The same principle applies when multiplying more than two fractions. For example, if you want to find 1/2 of 2/3 of 3/4:
1/2 × 2/3 × 3/4 = (1 × 2 × 3) / (2 × 3 × 4) = 6/24
Simplify the fraction:
6/24 = 1/4
Fractions with Mixed Numbers
If you encounter mixed numbers (e.g., 1 1/2), convert them to improper fractions before multiplying. For example, to find 2/3 of 1 1/2:
Convert 1 1/2 to an improper fraction:
1 1/2 = (1 × 2 + 1) / 2 = 3/2
Now, multiply:
2/3 × 3/2 = (2 × 3) / (3 × 2) = 6/6 = 1
Algebraic Representation
In algebra, fractions can be represented by variables. For example, if ( x = \frac{2}{3} ), then finding 2/3 of ( x ) would be:
2/3 * x = 2/3 * (2/3) = 4/9
FAQ Section
Q: What does "of" mean in math?
A: In mathematics, "of" usually means multiplication.
Q: How do you multiply fractions?
A: Multiply the numerators together to get the new numerator, and multiply the denominators together to get the new denominator.
Q: Can you simplify fractions before multiplying?
A: Yes, simplifying fractions before multiplying can make the calculation easier.
Q: What if I have a mixed number?
A: Convert the mixed number to an improper fraction before multiplying.
Q: Why is it important to understand fractions?
A: Understanding fractions is crucial for various real-life applications, including cooking, baking, construction, and finance.
Q: How do I convert cups to tablespoons?
A: 1 cup = 16 tablespoons. Multiply the number of cups by 16 to convert to tablespoons.
Q: How do I convert cups to milliliters?
A: 1 cup ≈ 236.59 milliliters. Multiply the number of cups by 236.59 to convert to milliliters.
Conclusion
Calculating 2/3 of 2/3 cup involves understanding the basic principles of fraction multiplication. By following the step-by-step instructions, practical examples, and tips provided in this guide, you can confidently solve this type of problem and apply it to various real-world scenarios. Whether you're scaling recipes, measuring ingredients, or solving mathematical problems, a solid understanding of fractions is an invaluable skill. Remember to practice and apply these concepts to reinforce your understanding and improve your proficiency. With this knowledge, you’re well-equipped to tackle any fractional challenge that comes your way.
Latest Posts
Latest Posts
-
And Never The Two Shall Meet
Dec 06, 2025
-
I Dont Care About What You Say
Dec 06, 2025
-
What Is A Scrub In Slang
Dec 06, 2025
-
Is Heathcliff Black In Wuthering Heights
Dec 06, 2025
-
How Do You Spell Taco In Spanish
Dec 06, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 Of 2/3 Cup . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.